Tout ce que vous avez toujours voulu connaître sur la cartographie ... sans jamais avoir osé le demander !
Bon OK, je le concède, ce sous-titre relève du plagiat pur et simple : Woody Allen l'a déjà utilisé, mais pour un sujet bien plus léger.
Quant à nous, nous allons essayer de comprendre - sans toutefois prétendre à faire un cours magistral - ce que sont les systèmes cartographiques, et tenter de s'y retrouver avec les coordonnées géographiques que l'on rencontre bien souvent au fil des inventaires spéléologiques et autre littérature spécialisée.
A - QUE DOIT-ON REPRESENTER ?
Wikipedia nous indique que la cartographie désigne la réalisation et d'étude des cartes géographiques, son objet est donc de représenter la terre : pour ce faire, elle doit faire appel à la géodésie c'est à dire la science qui s'est attachée à résoudre le problème de la détermination de la forme et de la dimension de la terre.
Sans faire un exposé complet d'histoire des sciences, il est maintenant acquis - sauf peut-être pour quelques adeptes de la théorie créationniste, quelque pastafariste ou encore tout lecteur crédule de Terry Pratchett - que la terre n'a pas été créée en 6 jours, qu'elle n'est pas plate et qu'elle tourne et ne repose pas sur 4 éléphants eux-même posés sur le dos de la tortue géante A'Tuin : mais qu'en est-il de sa forme exacte ?
En fait, du fait de sa rotation, elle n'est pas non plus tout à fait ronde : elle se rapprocherait plutôt d'une ellipse aplatie aux pôles, et c'est cette représentation mathématique de la terre qui est retenue en géodésie, sous le terme d'ellipsoïde (on y reviendra plus tard).
Mais c'est pas fini ! La surface terrestre n'est pas conforme à la représentation mathématique que la géodésie veut en faire : sa composition n'est pas uniforme (différences de densités entre le noyau, le manteau et la croûte terrestre ou océanique) et elle présente des reliefs prononcés (mers, océans, montagnes), ces différences influant sur la pesanteur s'appliquant en chacun des points de la surface terrestre. Il a donc été défini une surface fictive déduite de cette valeur de la pesanteur en tout point : le géoïde, permettant de représenter à un instant donné la surface gravimétrique de la Terre.
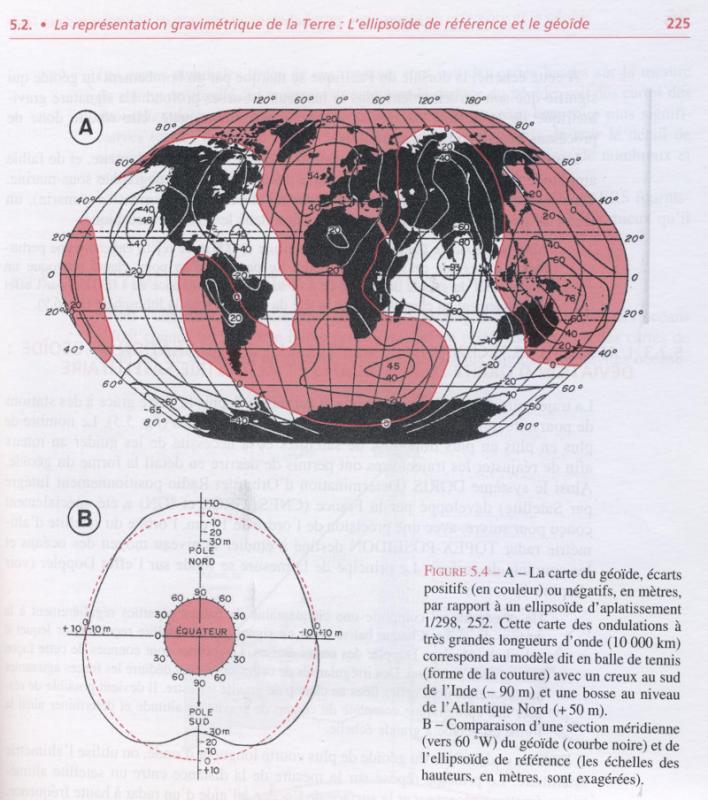
Pour mesurer exactement la forme du géoïde, il faudrait donc à un instant t mesurer en tout point du globe terrestre la verticale (donnée par la direction du fil à plomb), en déduire l'horizontale (définie comme la direction perpendiculaire à la verticale), et procéder ainsi de proche en proche afin d'obtenir une section de la terre en restant sur une horizontale : on pourrait mesurer ainsi une surface équipotentielle de pesanteur qui permettrait de décrire parfaitement le géoïde qui correspond donc à la forme gravimétrique de notre planète (cf. figure ci-dessus)
Or, mesurer ainsi le géoïde s'avère, dans la pratique, impossible et la cartographie va en fait se contenter de l'approximation mathématique introduite par la notion d'ellipsoïde afin de servir de référence aux mesures. Pour rappel, un ellipsoïde est donc le volume obtenu par la révolution d'une ellipse, dont l'aplatissement est défini par le rapport (a-b) / a, où a et le rayon équatorial et b le rayon polaire. Malheureusement, chaque service cartographique a défini son propre ellipsoïde de référence en fonction de la facilité d'emploi par rapport à son propre territoire national, c'est à dire la meilleure coïncidence de la surface théorique de l'ellipsoïde avec le territoire concerné.
Ainsi, historiquement la France utilisait l'ellipsoïde de Clairaut (qui est tangent à la surface terrestre à Paris : Place du Pathéon) et s'avère assez éloigné de la surface du continent américain sur lequel on utilisait une autre définition, l'ellipsoïde de Hayford.
Depuis 1965, les campagnes de géodésie spatiale ont malgré tout permis de définir le standard actuel : le système géodésique de référence GRS (pour geodesic Reference System) dont l'ellipsoïde est définie par un rayon équatorial de 6.378.136 mètres (∓ 1m) et un rapport d'aplatissement de 1/298,257 (∓ 0,001), et qui est utilisé par le système GPS (Global Positioning Surface).
B - Les systèmes et réseaux géodésiques
Maintenant que nous avons à peu près cerné toute la complexité l'objet à mesurer, et introduit une méthode de simplification avec la notion d'ellipsoïde, il nous reste à comprendre comment tout celà est utilisé.
Comme dit plus haut, chaque service cartographique avait défini ses propres méthodes de travail, et déterminé les paramètres géométriques les mieux adaptés à l'établissement des cartes de leur ressort. De ce fait, pour être compréhensible, toute coordonnée géographique devrait faire référence au système géodésique pour lequel elle est exprimée.
Historiquement, il sera possible de distinguer 2 type de systèmes géodésiques, discriminés suivant la méthode de réalisation :
- Les systèmes locaux : réalisés à partir de mesures terrestres selon la méthode de la triangulation qui consiste en mesurer des angles de triangles déterminés sur le terrain à cartographier, ainsi que quelques distances permettant de calculer la mise à l'échelle.
- Les systèmes spatiaux : bien évidemment plus récents, et basés sur des mesures satellitaires, définissant des constantes fondamentales (caractéristiques de l'ellipsoïde associée), coordonnées tridimensionnelles (longitude, latitude, hauteur ellipsoïdale) et précision du centre.
Dans tous les cas, un système géodésique qui doit permettre de déterminer le positionnement des points dans l'espace et le temps au voisinage de la terre, est un repère affine défini par son origine (le point fondamental, situé à proximité du centre des masses de la Terre) et par un point de la croute terrestre quasiment fixe (aux fluctuations des marées terrestres, à la surcharge océanique ou aux mouvements tectoniques globaux près) appelé point de référence.
Afin de minimiser les erreurs et éventuellement pallier aux possibles déformations, il est également généralement défini un réseau géodésique associé au système utilisé. C'est un ensemble de points physiquement liés à la croûte terrestre (bornes, piliers, etc...) disposés sur l'étendue du territoire à cartographier pour lesquels les services cartographiques ont décrit la position définie par des coordonnées estimées et leur variation, afin d'en déterminer les algorithmes devant intervenir dans le processus d'estimation des coordonnées.
Tableau récapitulatif des systèmes en usage en France :
| Systèmes locaux | Systèmes spatiaux |
|---|---|
|
Principes mis en œuvre : précision du centre des masses terrestres: quelques centaines de mètres |
Principes mis en œuvre : Précision du centre des masses terrestres : quelques mètres. |
| Réalisations historiques en France : - triangulation de Cassini (1733-1770) - triangulation des Ingénieurs Géographes (1792-1884) |
Systèmes mondiaux : - WGS84 (World Geodetic System 1984) - ITRS (International Terrestrial Reference System) |
| Système européen : - ED50 (European Datum 1950) |
Système européen : - ETRS89 (European terrestrial Reference System 1989) |
| Système actuel en France : - NTF (Nouvelle Triangulation de la France) |
Système actuel en France : - RGF93 (Réseau Géodésique Français) |
C – Caractéristiques de systèmes usuels
Quelques noms de systèmes sont à retenir, soit parce qu'ils sont utilisés en France, par l'IGN, ou au niveau mondial.
C1 - La Nouvelle Triangulation de la France (NTF) :
La NTF, développée par l'IGN, poursuit l'objectif de la réalisation de la cartographie du territoire national français à moyenne échelle. Elle est décrite par les caractéristiques géographiques suivantes :
-
Point fondamental : Croix du Panthéon à Paris.
-
Ellipsoïde associée : Clarke 1880 IGN.
-
Représentation plane associée : Lambert (4 zones)
-
Méridien origine : Paris.
La NTF est matérialisée sur le terrain par un réseau géodésique associé hiérarchisé, constituant un maillage intense du territoire :
-
- Le réseau principal, constitué de :
-
800 points de 1er ordre espacés d'environ 30 Km.
-
5.000 points de 2° ordre espacés de 10 Km environ,
-
60.000 points de 3° et 4° ordre espacés de 3 Km environ.
-
- Le réseau complémentaire, comptant 20.000 points de précisions diverses.
C2 – Le système European Datum 1950 (ED50) :
Mis en place à la suite de la seconde guerre mondiale, il a été établi grâce aux réalisation géodésiques de diverses nations d'europe occidentale. Ses caractéristiques sont les suivantes :
-
Point fondamental : POSTDAM.
-
Ellipsoïde associée : 1909.
-
Représentation plane associée : Universal Transverse Mercator (UTM)
Le modèle a par la suite subi plusieurs autres réalisations effectuées en variant les modes de calcul et d'observations prises en compte, notamment la dernière réalisation ED87 qui utilise des observations spatiales.
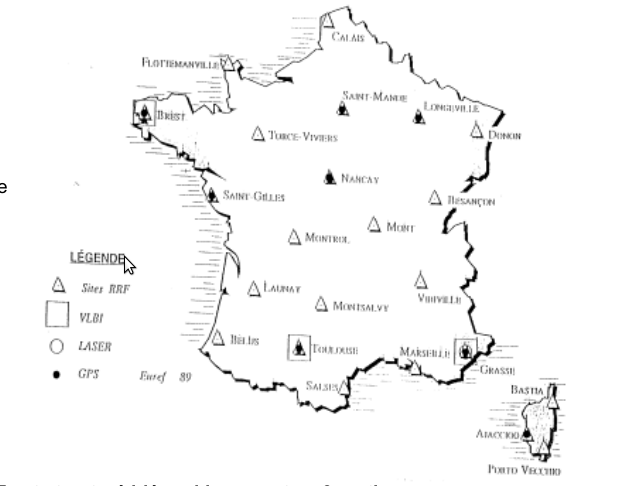
C3 – Le Réseau Géodésique Français 1993 (RGF93) :
Ce nouveau système, tridimensionnel et géocentrique, est établi par l'IGN par densification des points européens du réseau mondial associé ETRS89 (cf. infra).
Le réseau est structuré hiérarchiquement en 3 parties :
-
Le Réseau de Référence Français (RRF) : constitué de 23 points déterminées par géodésie spatiale de grande précision (10-7) sur la période allant de 1989 à 1993.
-
Le Réseau du Base Français (RBF) : 1009 sites déterminés par technique GPS (précision 10-6) sur la période allant de 1994 à 1996.
-
Le Réseau de Détail Français (RDF) : constitué de points de la NTF et de canevas géodésiques appuyés sur le RBF, encore en cours de réalisation.
Les coordonnées sont exprimées dans le système RGF93, soit sous forme tridimensionnelle géographique (longitude, latitude, hauteur ellipsoïdale), soit sous forme bi-dimensionnelle, selon la projection Lambert 93, unique pour l'ensemble du territoire (ce qui constitue un net progres par rapport aux 4 zones Lambert associées à la NTF).
C4 – Le système World Geodetic System 1984 (WGS84) :
Mis au point par le Département de la Défense des Etats-Unis d'Amérique, il est utilisé pour exprimer les éphémérides radiodiffusées du GPS. Ses caractéristiques sont les suivantes :
-
Ellipsoïde associée : IAG-GRS80
-
Représentation plane associée : UTM
-
Méridien origine : Greenwich
Son exactitude est de l'ordre du mètre sur l'ensemble du globe, et c'est donc le système utilisé nativement par tout GPS !
C4 – Le système International terrestrial Rotation Service (ITRS) :
Défini par l'International Earth Rotation Service (IERS), il est matérialisé par un réseau de quelques 300 points disséminés sur l'ensemble du globe.Son exactitude au niveau centimétrique en fait le plus précis des systèmes géodésiques mondiaux, et du fait de cette précision extrême, l'IERS fournit depuis 1988 une réalisation annuelle appelée ITRFyy (où yy correspond aux derniers chiffres du millésime), le dernier en date est ITRF97.
C5 – Le système European terrestrial Reference System 1989 (ETRS89) :
Ce système est défini à partir de l'ITRS et coïncide avec ITRS à l'époque 1989.0 mais est attaché à la partie stable de la plaque eurasienne.
La cohérence avec WGS1984 est métrique.
D – conclusion provisoire
Un point sur le globe terrestre (ou du moins sa position sur l'ellipsoïde qui le modélise théoriquement) peut donc être référencé par ses coordonnées géodésiques, lesquelles peuvent prendre la forme de :
-
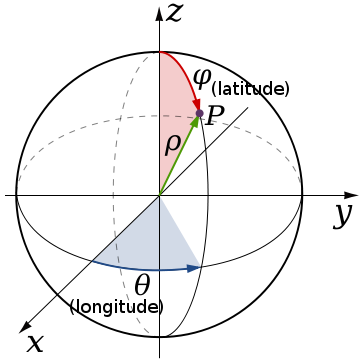
Coordonnées géographiques : données angulaires (latitude, longitude) et, éventuellement, hauteur ellipsoïdale.
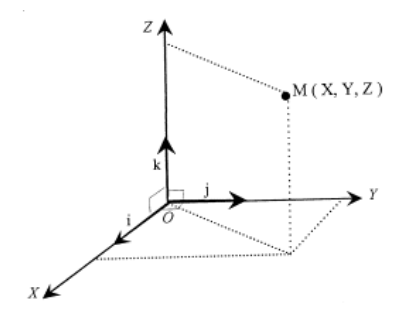
-
Coordonnées cartésiennes tridimensionnelles : X, Y et Z prises dans le repère orthonormé dont l'origine correspond au point origine de l'ellipsoïde su système utilisé.
Il ressort de ce qui précède que les coordonnées géodésiques d'un point ne sont pas des données objectives référentes au seul point mesuré mais sont relatives à un modèle théorique du territoire à représenter. Ainsi, disposer de coordonnées géographiques d'un point ne permet pas forcément de le localiser : il faut leur associer le référentiel géodésique dans lequel elles ont été relevées !

