Après avoir à peu prés cerné, dans le précédent article, la problématique des systèmes de référence géodésique, voici le second et dernier article de vulgarisation concernant la cartographie qui va introduire la notion de projection cartographique et essayer de faire le point sur l'utilisation des coordonnées.

A - Les projections cartographiques

La problématique essentielle de la cartographie est qu'on cherche à représenter sur une surface plane (généralement, une carte imprimée sur une feuille de papier) l'image d'un object assimilé à un ellipsoïde afin de permettre d'effectuer des mesures directes grâce aux cordonnées ainsi obtenues : il est en effet difficile de mesurer avec une règle une distance sur un globe planétaire, tout comme il serait peu pratique d'essayer de se repérer sur le terrain avec un tel objet...

La première technique venant à l'idée serait de reporter directement des coordonnées géographiques sur une carte papier (obtention de coordonnées planes), mais cette méthode comporte un biais rédhibitoire : l'objet représenté sera déformé et les distances non conservées.
Les mathématiques sont donc venues au secours des cartographes avec les techniques de projection qui permettent, d'associer à tout point du globe son image sur un plan. Sans entrer dans les détails, trois principaux types de projection sont utilisés en cartographie :

Projection cylindrique

La surface de projection est un cylindre englobant l'ellipsoïde à représenter :

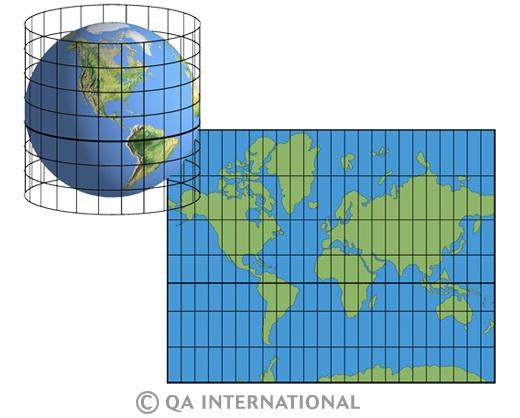
Selon l'orientation du cylindre de représentation, la projection est nommée cylindrique directe, oblique ou traverse :

 

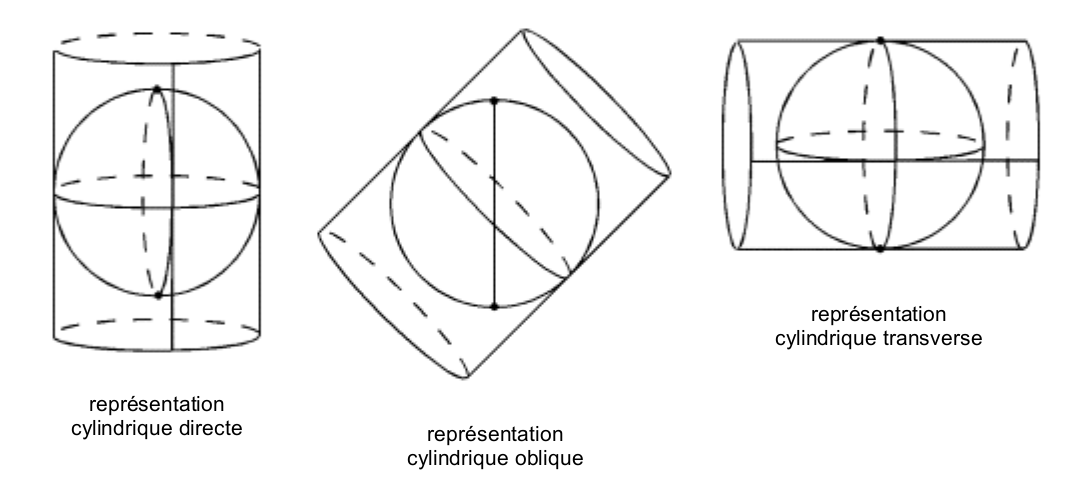
Projection conique

La surface de projection est un cône tangent ou sécant  :

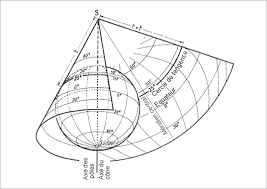
Projection azimutale

La surface de projection est un simple plan :

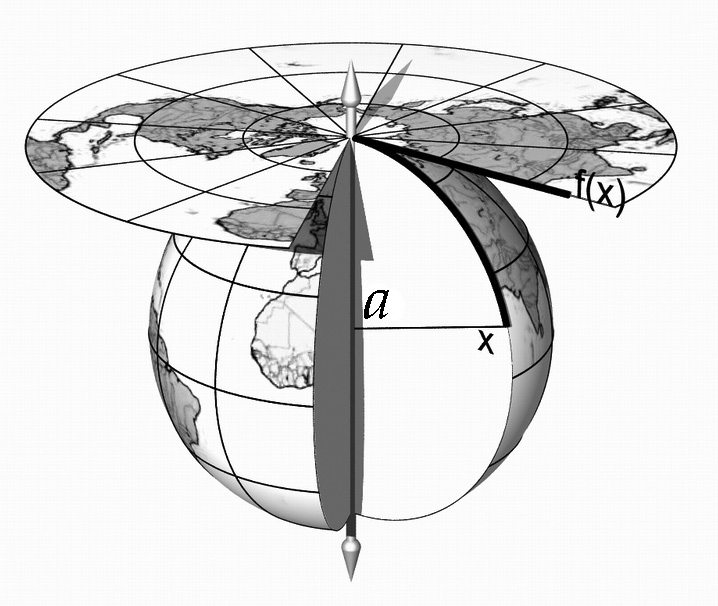
Au final, après projection, on obtient une image du territoire à représenter qui conserve les distances et présente – pour peu que les paramètres soient correctement choisis – un taux de distorsion acceptable.

→A retenir : il existe deux types de coordonnées :

• Les coordonnées géographiques, représentant la mesure angulaire d'un point directement situé sur l'ellipsoïde (par rapport au système géodésique choisi).

• Les coordonnées planes, représentant la position d'un point dans un repère cartésien choisi sur la projection de l'ellipsoïde.

 

B – Les systèmes de coordonnées fréquemment utilisés en France

Le système GPS, comme vu précédemment, fournit par défaut des coordonnées géographiques exprimées par :

- une latitude (positionnement du point sur un parallèle) généralement exprimée en degrés par rapport à l'équateur (valeur positive dans l'hémisphère nord et négative dans l'hémisphère sud).

- une longitude (positionnement du point sur un méridien ) généralement exprimée en degrés par rapport au méridien origine de Greenwich (valeur positive à l'est du méridien de Greenwich, négative à l'ouest).

- une hauteur ellipsoïdale, à ne pas confondre avec l'altitude, qui est la distance entre le point et la surface de l'ellipsoïde de référence.

 

Pour ce qui est des coordonnées planes l'IGN a défini pour la France ses propres systèmes de coordonnées, mais il est également courant d'avoir des points définis dans le système UTM.

 

Coordonnées Lambert :

Il s'agit du système historique utilisé par l'IGN, par projection conique conforme de Lambert associée au système géodésique NTF. Dans le but de minimiser les déformations, l'étendue du territoire français a été découpé en 4 zones (Lambert I, II, III et IV) et dont la composante Nord se différencie par le chiffre des millliers (en km) et une projection particulière appelée « Lambert II étendu » couvre la France entière, dont les paramètres sont :

 

Zone Lambert	I	II	III	IV	II étendue
Zone d'application	53,5gr - 57gr	50,5gr - 53,5gr	47gr - 50,5gr	corse	France Entière
Latitude origine	55gr = 49°30 ́	55gr = 49°30 ́	49gr = 44°06 ́	46,85gr = 42°09 ́54"	52gr = 46°48 ́
Longitude origine	0gr Paris	0gr Paris	0gr Paris	0gr Paris	0gr Paris
X0 (false easting)	600 000 m	600 000 m	600 000 m	234,358 m	600 000 m
YO (false northing)	200 000 m	200 000 m	200 000 m	185 861,369 m	2 200 000 m

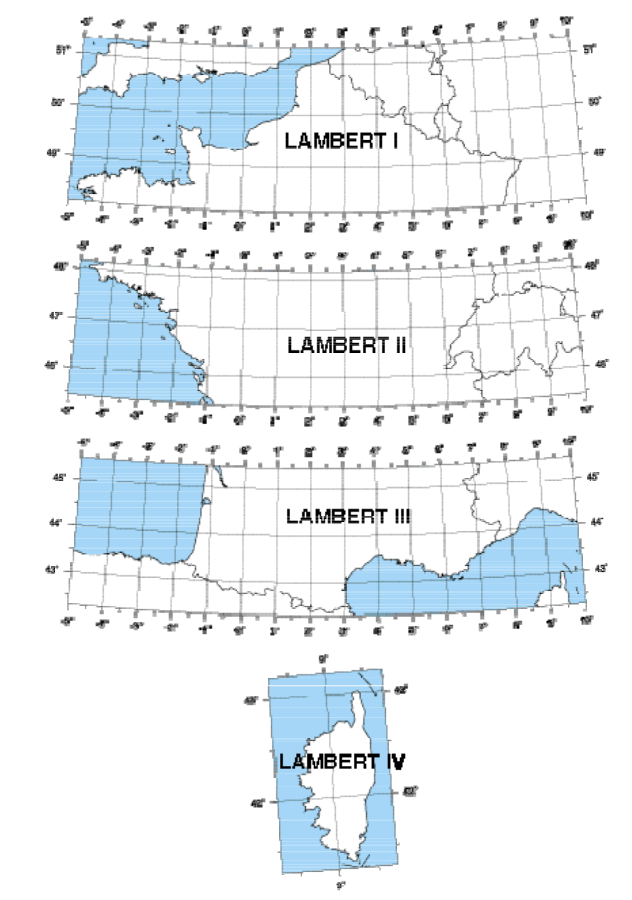
Ainsi, pour exemple les coordonnées du Barrenc du Pla de Périllos (en WGS84 : 42,8949° de latitude nord et 2.86725° de longitude Est) , exprimées en Lambert (donc en zone 3), seraient : X = 643349 et Y = 3066256 (ou, comme vu souvent, exprimées en kilomètres, X = 643,349 et Y = 3066,256).

A noter, la composante Nord, prend pour la zone 3 un chiffre des milliers ayant pour valeur la zone, soit 3 !

De même, en lambert II étendu, cela donne : X = 643437 et Y = 1765903 (en mètres)

 

Coordonnées Lambert93 :

Ce nouveau système de coordonnées a été retenu comme le système légal français à partir de septembre 1996.
Il s'agit d'une projection sécante de Lambert basée sur le référentiel géodésique RGF93 avec pour ellipsoïdale associée IAG GRS80.

Son point d'origine est situé sur 46°30' N et 3°E / méridien de Greenwich, et les coordonnées sont établies avec un X0 (False Easting) de 700 000m et Y0 (False Northing 6 600 000m.

 

Son principal avantage est de ne pas nécessiter de découpage en zones, mais pour une grande précision, les conversions nécessitent d'utiliser une grille de déformations établie par l'IGN.

 

Les coordonnées du Barrenc, exprimées en Lambert93 :
X = 689146 et Y = 6199506 (en mètres)

 

Coordonnées UTM :

La projection UTM (Universal Transverse Mercator) est une projection cylindrique qui couvre l'ensemble du globe, mais est constituée de 60 fuseaux de 6 degrés d'amplitude en longitude afin d'éviter de trop grosses déformations sur l'axe de X ; son système géodésique associé est ED50 et son ellipsoïde associée est International (Hayford 1909).
Il s'agit d'un système de coordonnées couramment utilisé par les services géographiques nationaux, et notamment le système légal en Espagne et Catalogne.

Le territoire français est couvert par 2 zones de projection UTM : les fuseaux Nord 30 à 32 :

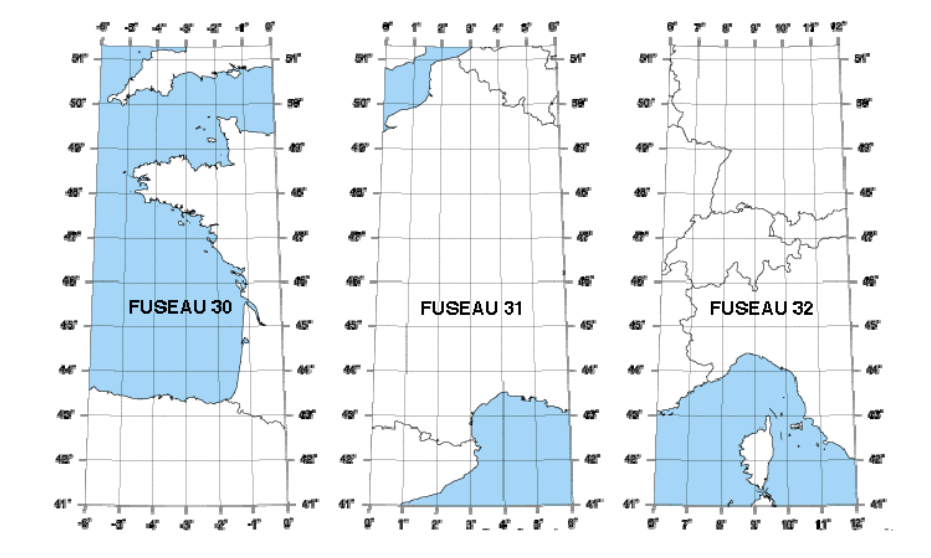
Les coordonnées du Barrenc exprimées en UTM (donc, fuseau Nord 31) :

X = 489253 et Y = 4749354 (en mètres)

 

C – L'altitude :

Comme vu au dessus, la composante Z des coordonnées géographiques est la hauteur par rapport à l'ellipsoïde de référence, et ne peut en aucun cas être assimilée à l'altitude, qui est une mesure tout à fait arbitraire pour un territoire donné.

En France, le référentiel d'altitude 0m est donné par une campagne de mesures du niveau moyen des marées de la mer Méditerranée au marégraphe de Marseille entre 1962 et 1969 : c'est à partir de ce point qu'a été établi le réseau de nivellement français de l'IGN (pour la Corse, le référentiel 0m est déterminé par le marégraphe d'Ajaccio).

A partir de ce point de repère fondamental, l'altitude légale est mesurée de proche en proche, et tout un réseau de repères altimétriques a été mis en place sur l'ensemble du territoire français, constituant le réseau du nivellement général de la France (NGF), d'où le suffixe NGF souvent apposé à une information d'altitude.

En conclusion, la composante altitude ne pourra directement pas être déduite d'une mesure de position par GPS, mais relevée sur la carte topographique après positionnement du point grâce aux coordonnées obtenues.

 

D – Conversion de coordonnées :

La conversion de coordonnées d'un système géodésique vers un autre nécessite pas mal de calculs et la connaissance de l'ensemble des paramètres de chacun des systèmes en jeu, que l'on peut toutefois retrouver sur internet, et notamment sur le site spatialreference.org.
Mais, dans tous les cas, mieux vaut faire appel à un logiciel spécialisé, parmi lesquels, je citerai :

• le vénérable proj4 (outil en ligne de commande pour Unix ou Windows, mais la référence absolue des conversions).

• convers, d'Eric David, par ailleurs auteur de Visual Topo, pour windows.

• convertisseur d'Eric Sibert, pour windows.

• Circé, le logiciel fourni gratuitement par l'IGN, pour windows.

Ou encore via des convertisseurs en ligne, tels que :

• Tools online

Au final, j'espère que cette petite série aura permis de faire face à la complexité de cette matière, et nous permetttra de déméler quelque peu la jungle des coordonnées cartographiques afin de parvenir à localiser sereinement sur le terrain nos cavités favorites.